目次
はじめに
ボリンジャーバンドは、多くのトレーダーが使う有名なテクニカル指標です。
ボリンジャーバンド(Bollinger Bands)は、ジョン・A・ボリンジャー(John A. Bollinger) が1980年代初頭に考案されました。
ボリンジャーバンド入門 ジョン・A・ボリンジャー (著)
初心者でも「価格の幅」を直感的にイメージできる一方で、統計学に基づいた理論背景を持っています。
本記事では、ボリンジャーバンドの仕組みを基礎から解説し、さらに統計的に正しいのかという点について検証してみます。
またボリンジャーバンドに似たパーセンタイルバンドについても紹介します。
最後には使い方も紹介します。
ボリンジャーバンドとは?
移動平均線と標準偏差を使ったテクニカル指標
ボリンジャーバンドは「単純移動平均線(SMA)」を中心に、上下に「価格のばらつき(標準偏差)」を描いたバンドです。価格がこの範囲に収まる確率を利用して、相場の状態を把握しやすくします。
「単純移動平均線(SMA)」については以下の記事を参照してください。
MAとMACDによるトレンド転換のメカニズムを図解|イメージでわかりやすく説明
下図は、2σ(標準偏差)で描いた事例となります。
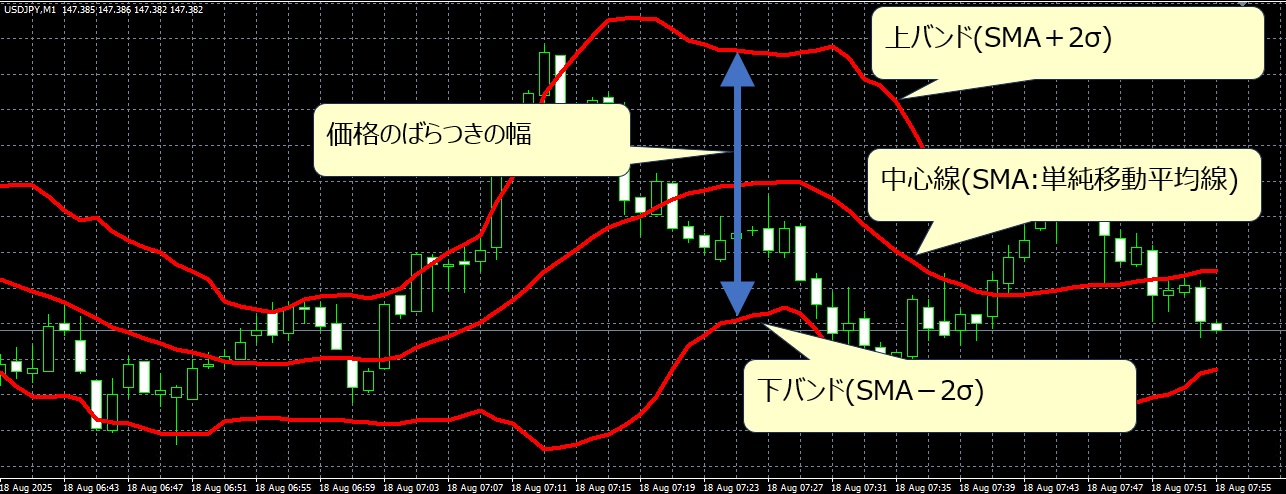
標準偏差を使う理由
ボリンジャーバンドが標準偏差を使う理由は、自然界の事象に正規分布が多く、そこから価格変動の確率的な幅を推定できるからとなります。
ただし、後で説明しますがFXにおける価格変動は必ずしも正規分布ではないため、完全に正規分布を仮定しているわけではありません。
価格の「ばらつき」を数値化する
標準偏差は、各データが平均値からどれくらい散らばっているかを表す指標です。
数式で表すと次のようになります。
簡単に言えば、平均値からのデータの距離の「平均のようなもの」とイメージできます。
実際には平方平均なので少し数学的な補正がありますが、直感的には「ばらつきの大きさ」を表す指標です。
標準偏差には次のような確率的な意味があります。
- ±1σ:データのおよそ68%がこの範囲に収まる
- ±2σ:データのおよそ95%がこの範囲に収まる
- ±3σ:データのおよそ99.7%がこの範囲に収まる
ボリンジャーバンドでは、この±σの幅を価格の上下に描くことで、値動きの範囲やトレンドの目安として活用されます。
ボリンジャーバンドは正規分布を仮定している?
「価格変動は正規分布する」という前提
ボリンジャーバンドは「単純移動平均値からの価格変動は正規分布に従う」という前提のもとで考案されています。
価格変動は正規分布に従うという前提は、正しいのでしょうか。
実データで検証してみた
価格のばらつきは正規分布か?
以下のデータでヒストグラムを作成してみました。
| 項目 | 内容 |
|---|---|
| 通貨ペア | ドル円 |
| データ分析の期間 | 2023年1月2日~2024年8月8日 |
| 時間足 | 1時間 |
| データ数 | 10,000件 |
| データ | EMA(単純移動平均値)-Close値 |
結果は、次の図の通りです。
ヒストグラムに正規分布を重ね合わせています。
どうでしょうか。
正規分布に見えなくもありませんが、中央の山が正規分布よりも尖がっているように見えます。
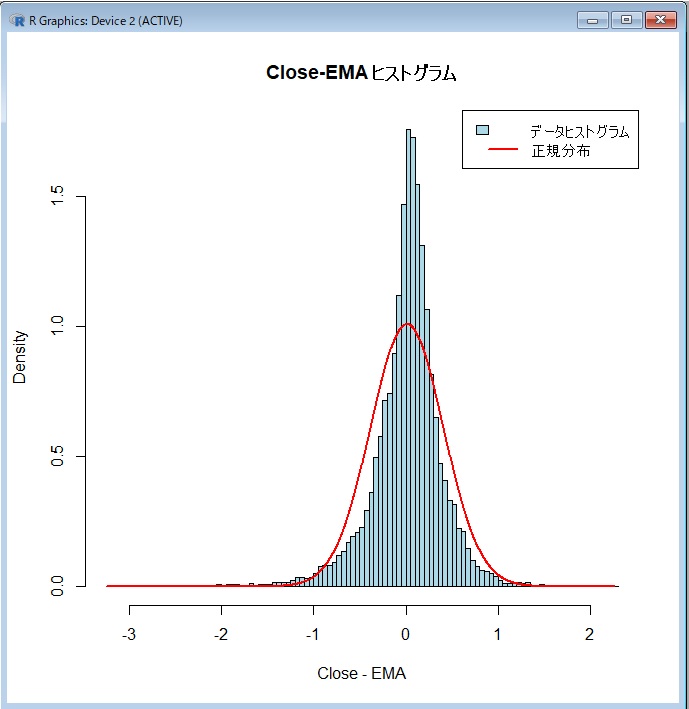
正規分布かどうかは、見た目だけで判断できないため、統計検定をしてみました。
正規分布かどうかは、Shapiro-Wilk(シャピロ・ウィルク)検定を使います。
結果は、次の通りです。(統計ソフトR言語を使用)
Shapiro-Wilk normality test
p値 < 0.00000000000000022
→ p値というのは「もし正規分布だったと仮定したら、こんなにデータが正規分布からズレる確率はどれくらいか?」という数字。
→ 小さいほど「正規分布じゃない」と判断できます。
→ ここでは 非常に小さい(ほぼ 0) なので、「正規分布ではない」と結論できます。
検定のルールは次の通りです
| 判定条件 | 解釈 |
|---|---|
| p値 > 0.05 | 正規分布とみなせる |
| p値 ≤ 0.05 | 正規分布ではない |
今回の結果は上記の検定ルールから、「単純移動平均値-Close」のデータのばらつきの分布は正規分布ではない と言えます。
上記の結果は、2023年1月2日~2024年8月8日の期間で分析した結果ですが、他の期間でも同様に正規分布ではないという結果になります。
時間足も1分、15分、30分、4時間、日足で検証しましたがやはり、正規分布ではないという結果になりました。

パーセンタイルバンドというテクニカル指標
価格変動が正規分布でない場合はどうすればよいのでしょうか。
分布の形状が不明な場合によく使われるのは、パーセンタイル(Percentile)という統計手法です。
パーセンタイルは、データを 小さい順に並べたときに「何%の位置にあるか」を示す値 です。
簡単に言うと:
上位95パーセンタイル → データを小さい順に並べたとき、上から5%に入る値
下位5パーセンタイル → データを小さい順に並べたとき、下から5%に入る値
つまり:
| パーセンタイル | 意味 |
|---|---|
| 50(中央値) | データの真ん中の値 |
| 95 | データの上位5%の値 |
| 5 | データの下位5%の値 |
このパーセンタイルを使用し、ボリンジャーバンドのようなことが可能です。
マイナーですが、パーセンタイルバンドというテクニカル指標です。

パーセンタイルバンドのインジケーターを自作し、ボリンジャーバンドとパーセンタイルバンドはどのくらい差があるのか、比較してみました。
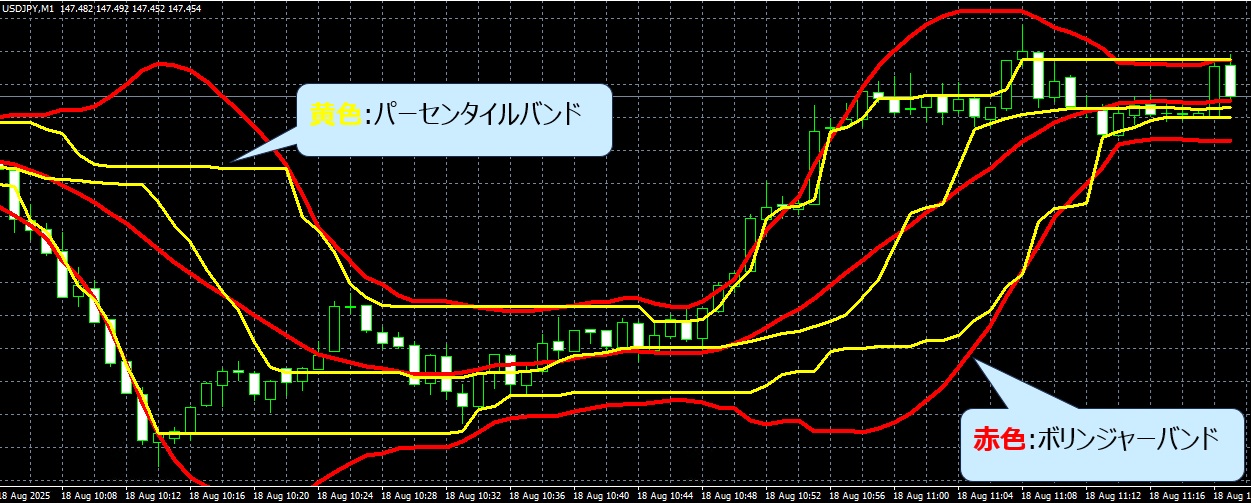
どちらも上下限は、5%~95%で計算した結果です。
似たようなグラフとなりましたが、赤色(ボリンジャーバンド)の方が黄色(パーセンタイルバンド)よりも広がる傾向があります。
また上昇トレンドの場合、黄色(パーセンタイルバンド)はほとんどバウンドウオークしています。
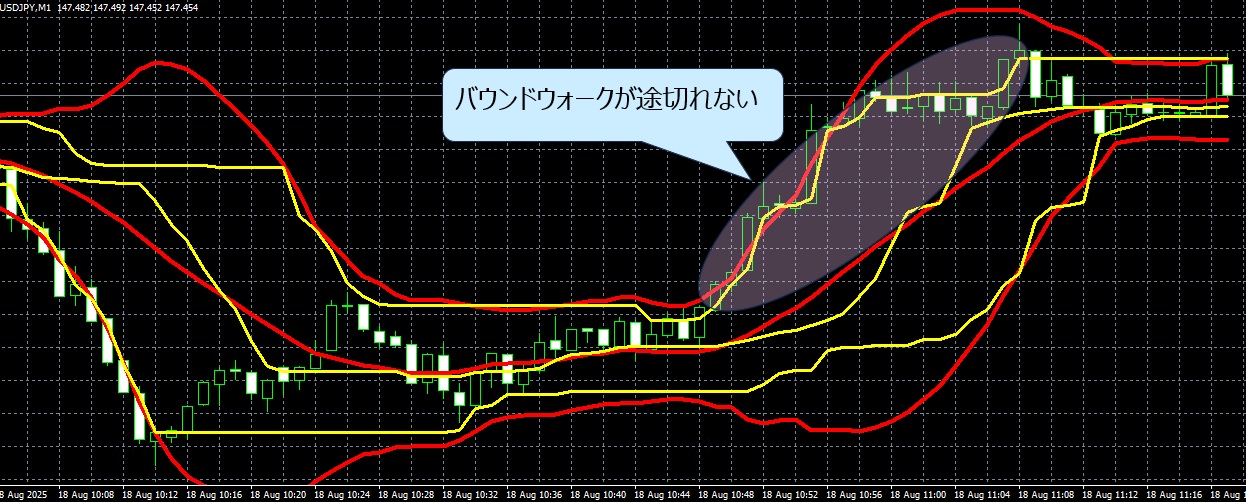
赤色(ボリンジャーバンド)は、バウンドウオークしていないところがあります。
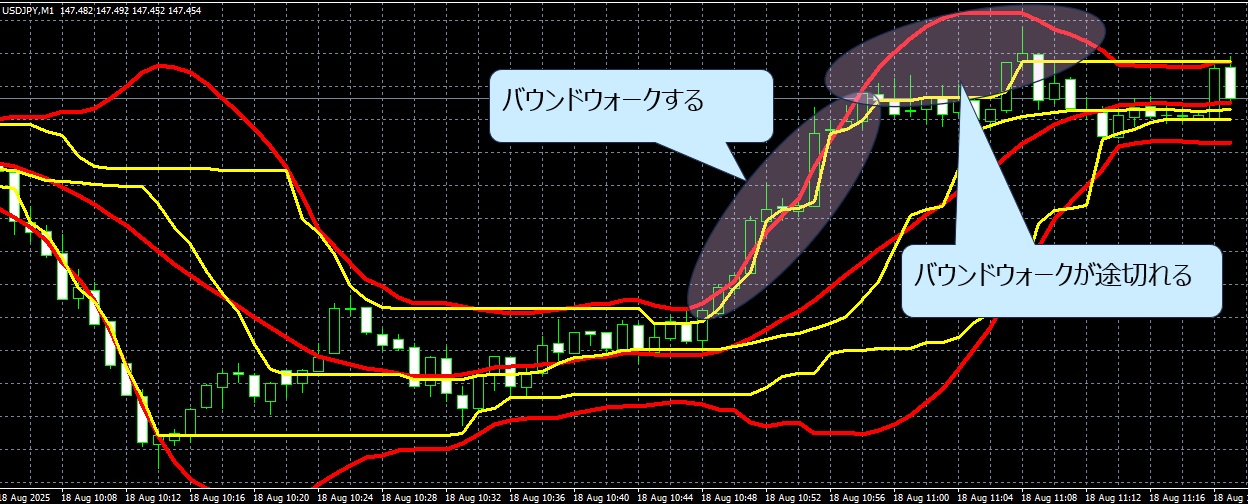
下降トレンドの場合も同様です。
レンジトレンドの場合は、赤色(ボリンジャーバンド)、黄色(パーセンタイルバンド)ともに似たような幅になります。
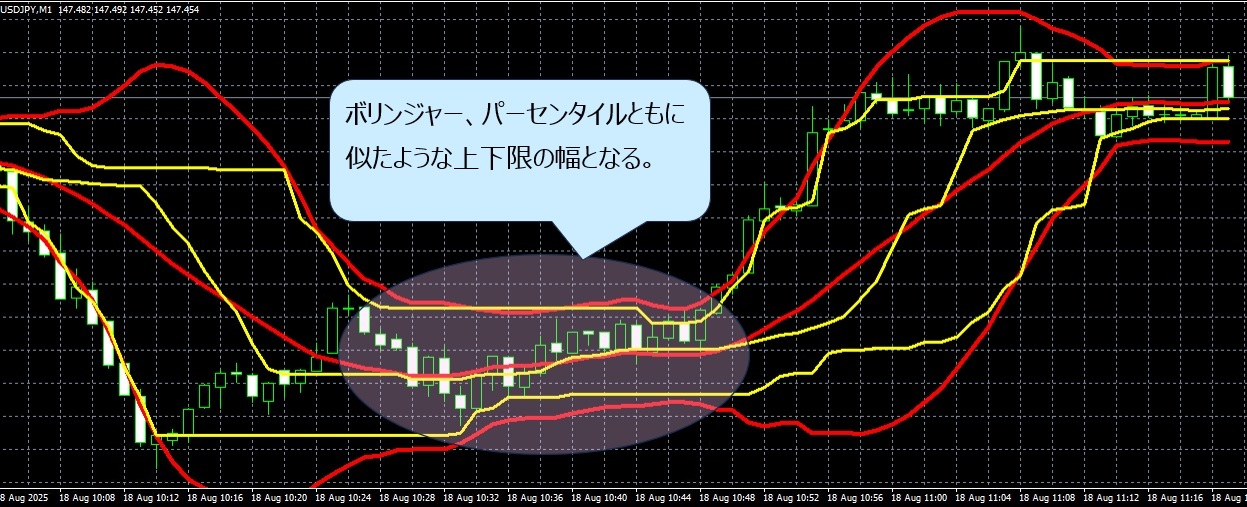
違いが出る原因は次の2つの特徴に集約されます。
| 特徴 | ボリンジャーバンド | パーセンタイルバンド |
|---|---|---|
| 外れ値の影響 | 極端な値に影響を受けやすく、その場合はバンドが大きく広がる。 | 外れ値の影響を受けにくいため、ボリンジャーより狭くなるケースも多い。 |
| 上下の形 | 正規分布に当てはめるため、バンド幅は上下対称になる。 | 本当の分布に基づいて算出するため、上下のバンド幅は非対称になることが多い。 |
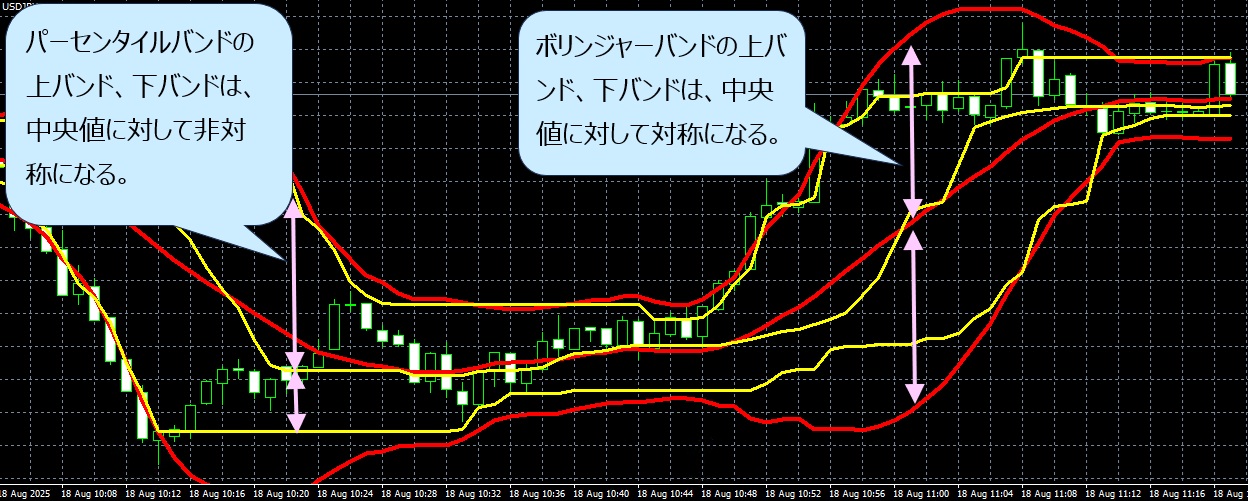
結果として
- トレンド中 → パーセンタイルはバンドウォークが続くがボリンジャーは途切れる
- 急変動 → ボリンジャーは広がりすぎる、パーセンタイルは比較的安定する
- レンジ → 両者とも似た幅となる
それぞれのメリット、デメリットを整理すると以下の表のようになります。
| 指標 | メリット | デメリット |
|---|---|---|
| ボリンジャーバンド | ・計算が簡単 ・多くのトレーダーに認知されている |
・外れ値に弱い ・相場の偏りを反映しにくい |
| パーセンタイルバンド | ・外れ値の影響を受けにくい ・データ分布を直感的に把握できる |
・計算が複雑 ・一般的でなく応用例が少ない |
実際は正規分布でなくても役立つ理由
「だいたい正規分布」で十分使える
相場データは完全な正規分布ではありません。
しかし、統計的に厳密でなくても、以下の2つの理由により有用であると思います。
- 正規分布とすることで標準偏差による上限値、下限値の算出が簡単である
- ボリンジャーバンドは、多くのトレーダーが使用しているため、このテクニカル指標自体が相場に影響している可能性がある
ボリンジャーバンドの代表的な使い方
ボリンジャーバンドの代表的な使い方を表にまとめてみました。
パーセンタイルバンドも使い方は基本的に同じです。
| バンドの種類 | 使い方 | 注意点 |
|---|---|---|
| ボリンジャーバンド | ①上昇トレンドの場合 上昇トレンドでは、上限バンドの上に価格があることが多く、トレンド継続の参考になります ②下降トレンドの場合 下降トレンドでは、下限バンドの下に価格があることが多く、トレンド継続の参考になります ③レンジ 線の上に価格があると反転し、価格が下落する可能性がある → 売りの目安として参考にする 線の下に価格があると反転し、価格が上昇する可能性がある → 買いの目安として参考にする ④線が狭くなると、これから価格が大きく動く可能性がある |
価格が強いトレンドのときは、逆張りに注意 |
まとめ
ボリンジャーバンドとパーセンタイルバンドは、どちらも価格の「高い・安い」を直感的に把握できる便利なテクニカル指標です。
ボリンジャーバンド:単純移動平均と標準偏差を使い、価格のばらつきやトレンドの変化を確認できます。
線の上に価格があると「価格が下落する可能性がある」、下にあると「価格が上昇する可能性がある」と目安になります。
パーセンタイルバンド:価格の分布位置を使い、極端な値に影響されにくく、価格の位置やレンジ感をより正確に判断できます。
どちらも実務上は十分に役立ちます。特に、ボリンジャーバンドは多くのトレーダーに使われているため、相場心理を反映することもあります。

