目次
はじめに
カーブフィッティングについて解説したサイトや書籍は数多くありますが、内容があまりにも専門的で、難解さゆえに挫折してしまう方も少なくないのではないでしょうか。
本記事では、まず「カーブフィッティングとは何か」を初心に立ち返って再確認し、そのうえで実用的な検証方法についてご説明します。
あくまで私自身の考察に基づくものであり、異論もあるかと思いますが、その点はあらかじめご容赦ください。
カーブフィッティングとは?
カーブフィッティングとは「曲線あてはめ」とも呼ばれる手法です。
ある区間のデータにうまく合うように曲線を当てはめますが、その曲線が区間外のデータにも当てはまるとは限りません。
むしろ、過剰に曲線を当てはめてしまうと、区間外のデータとは合わなくなってしまいます。
FXの世界では、これを「過剰最適化」あるいは「オーバーフィッティング」と呼ぶこともあります。
実験的に得られたデータまたは制約条件に最もよく当てはまるような曲線を求めること。
引用 Wikipedia「曲線あてはめ」
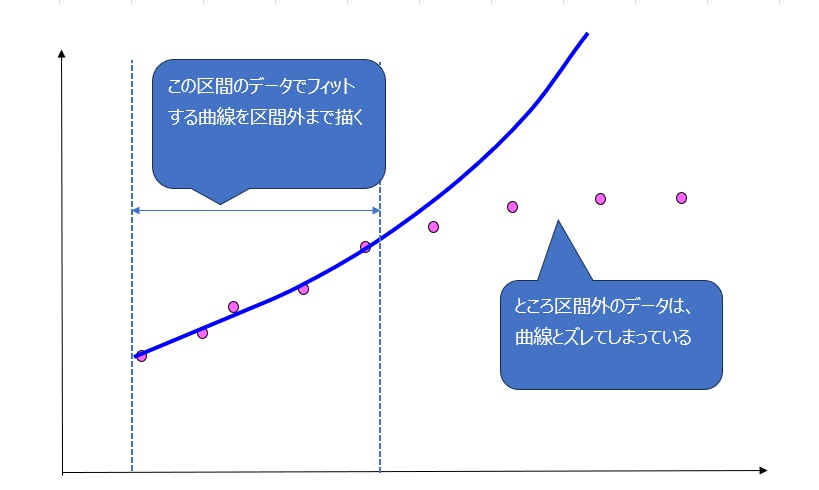
少し定義っぽく言うと、次のようになります。
「過去のあるデータにだけピッタリ合うように作られたトレードルールは、その期間以外では通用しにくい」
上図からイメージできるかと思います。
カーブフィッティングの種類
私は、カーブフィッティングには、主に次の2種類があると考えています。
- 特定の相場環境にだけマッチするトレードルール
例:2008年のリーマン・ショック時の急激な相場変動に特化したトレードルールは、その時期には効果が高いですが、他の期間では効果がありません。再び同様のショックがあれば有効かもしれません。 - 完全に偶然の一致であるトレードルール
例:過去5年間のデータで「土曜日に雨が多い年はドル円が円高になる」といった相関があったとしても、偶然の一致であり、今年の土曜日も雨が多いので円高になるとは限りません。
カーブフィッティングでないFXトレードルール
逆に、カーブフィッティングではないトレードルールとは、「過去のデータでうまくいった方法が、別のデータでもそれなりに通用する場合」のことを指します。
ただし「それなりに通用する可能性が高い」としか言えません。
なぜなら、たとえカーブフィッティングではないと判断できても、将来の相場で本当に通用するかどうかは誰にも分からないからです。
つまり、最終的に分かるのは「カーブフィッティングではない可能性が高い」というところまでで、それ以上は断言できないのです。
カーブフィッティングでないことを検証する方法
①検証データ数を多くする&期間を長くする&ルールはシンプルにする
・検証データ数は多くする
次の図のようにバックテストで使用する検証データが少ない場合、検証データの外では通用しない可能性が高くなります。
※注意 図はあくまで概念的なイメージです。横軸は時間、縦軸は値動きを表しています。FXのトレードルール自体は価格の予測ではありませんが、説明をシンプルにするため、図中の曲線は値動きの予測として描いています。これ以降も同様の図が登場しますが、同じように「イメージ」としてご覧ください。

感覚的にも分かると思いますが、次の図のように検証データを多くするほど、検証データ外でも通用する可能性は高くなります。(※冒頭の注意参照)
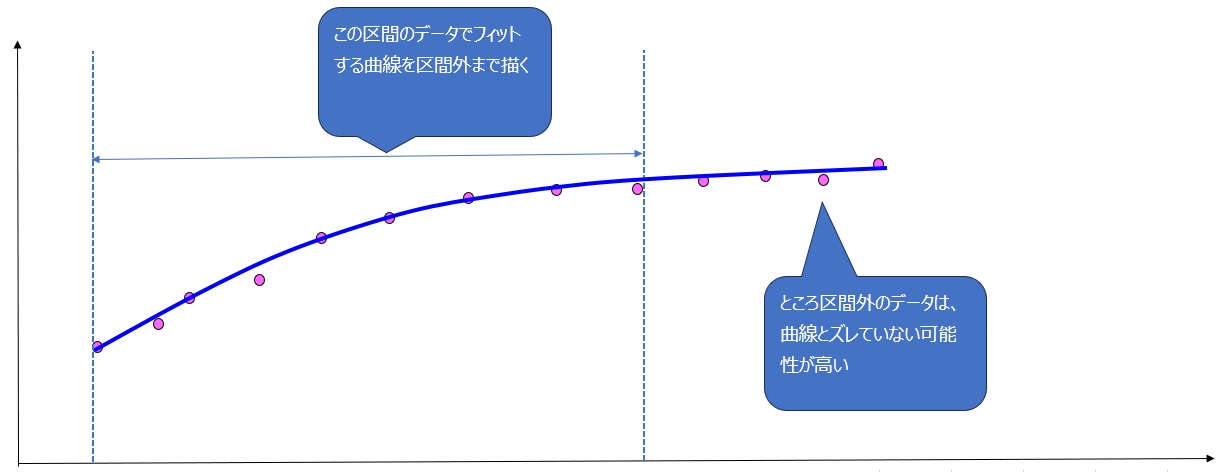
・期間は長くする
過去20年間でFX相場に影響があった出来事です。
| 期間 | イベント | 主な出来事 | 相場への影響(例) |
|---|---|---|---|
| 📉 2007–2009 | リーマン・ショックと世界金融危機 |
|
世界的株安・リスク回避で円高(USD/JPY 124円台→87円台) |
| 💴 2011 | 東日本大震災と円高急騰 |
|
USD/JPY 一時75円台 |
| 📈 2012–2015 | アベノミクス&黒田バズーカ |
|
USD/JPY 75円台→125円台へ上昇 |
| 💵 2015 | スイスフランショック |
|
急変動で多くの損失発生 |
| 🇬🇧 2016 | Brexit(英国のEU離脱国民投票) |
|
GBP急落、為替市場が大混乱 |
| 🇺🇸 2018–2019 | 米中貿易戦争 |
|
安全資産志向で円高・ドル高が進行 |
| 🦠 2020 | コロナ・ショック |
|
「ドル高・円高」が同時進行 |
| 💹 2021–2023 | 米国の急速利上げ(インフレ対応) |
|
米ドル独歩高(USD/JPY 一時151円超) |
| 💣 2022 | ロシアのウクライナ侵攻 |
|
EUR下押し、資源国通貨(AUD/CAD)相対的に強含み |
| 📊 2024–2025 | 米大統領選挙、世界的インフレと金融政策の転換 |
|
為替は不安定化・乱高下 |
FXを取り巻く相場環境は、この20年間を見ても大きく変動を繰り返してきました。
こうした様々な局面で通用するトレードルールを作らなければ、特定の相場環境にしか効かない「カーブフィッティング」になってしまいます。
そのため、検証に使う期間はなるべく長くとることが大切です。
ただし、あまりに古いデータは現在の市場環境とかけ離れている場合もあるため、長期と直近のデータをバランスよく組み合わせるのが現実的です。
では、具体的にどのくらい前からのデータを使うべきでしょうか。
検証データのサンプルが1000件以上取れる場合は、過去5年間くらいの期間でも十分でしょう。
一方、サンプルが1000件未満の場合は、もう少し長めの期間を使った方が良いかもしれません。
結局のところ、このあたりは「期間の長さ」と「データ量」のバランスによる判断になります。
・トレードルールはシンプルにする
FXのトレードルールについて複雑になればなるほど、カーブフィッティングの可能性が高くなると言われています。
イメージでは次の通りです。
次の図は、シンプルかつカーブフィッティングでないケースです。(※冒頭の注意参照)
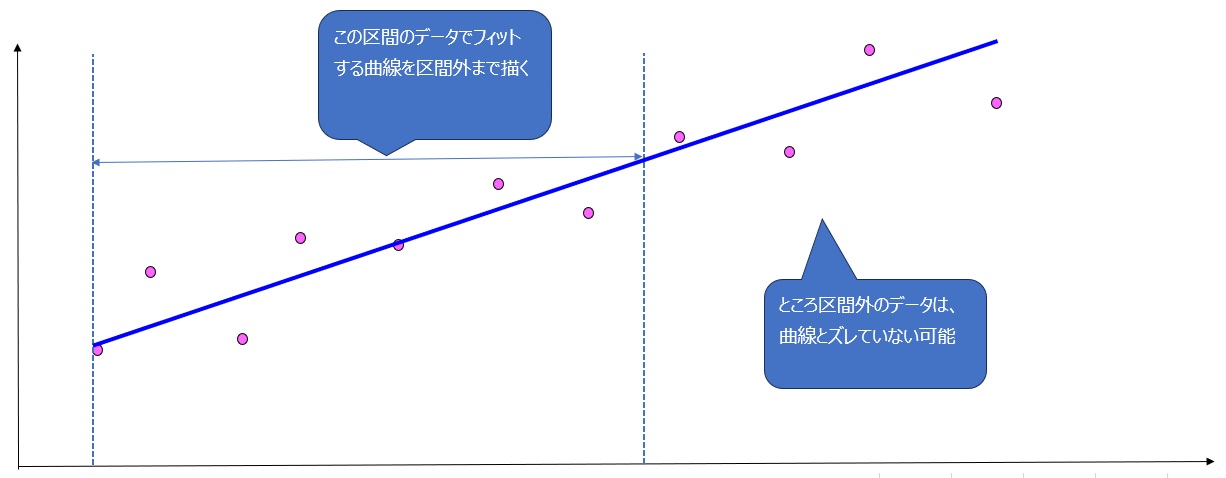
このデータでパラメータが多いトレードルールを作ったとします。
数式で表現すると次の通りです。
\(y = f(x_1, x_2, x_3, \dots, x_n)\)
数学的には、パラメータが多いほど、複雑で「ぐにゃぐにゃ」とした曲線に過去データをフィットさせることが可能です。
極端な話、無限にパラメータがあれば、すべての価格変動に合わせたトレードルールを作ることも可能です。
しかし、次の図のように、検証データの外ではうまく通用しない可能性が高くなります。(※冒頭の注意参照)
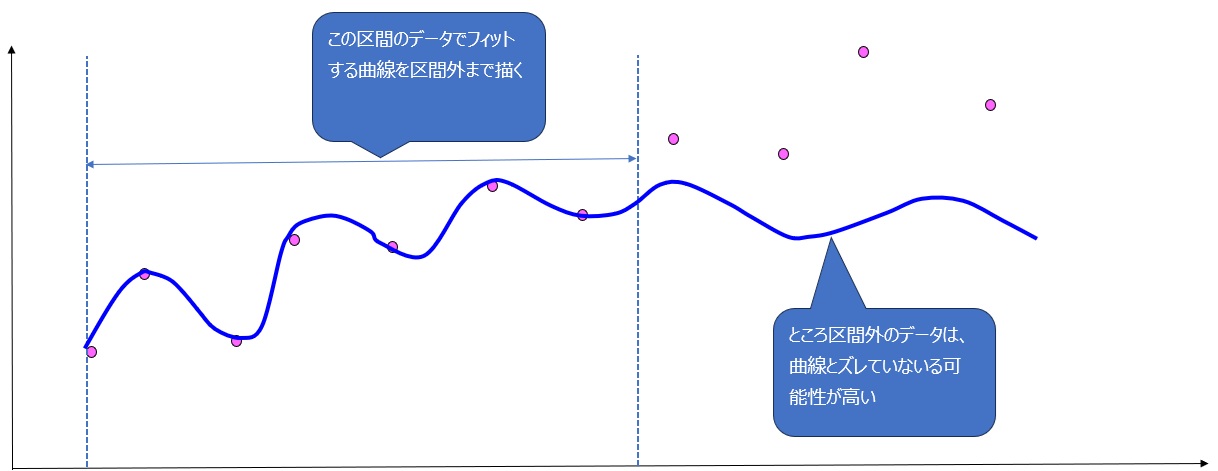
パラメータ数が多いからといって、必ずしもカーブフィッティングになるわけではありません。
FXの相場環境は、さまざまな要因で複雑に変動しています。
そのため、こうした要因を考慮すると、トレードルールも必然的に複雑化していきます。
ただし、複雑化には「必要最低限であること」が重要です。
パラメータの値の幅が狭いのもいけないとされています。
例えば、以下の図のようにパラメータの値を少しずらしても結果があまり変わらない場合です。(※冒頭の注意参照)
これが理想的なトレードルールです。
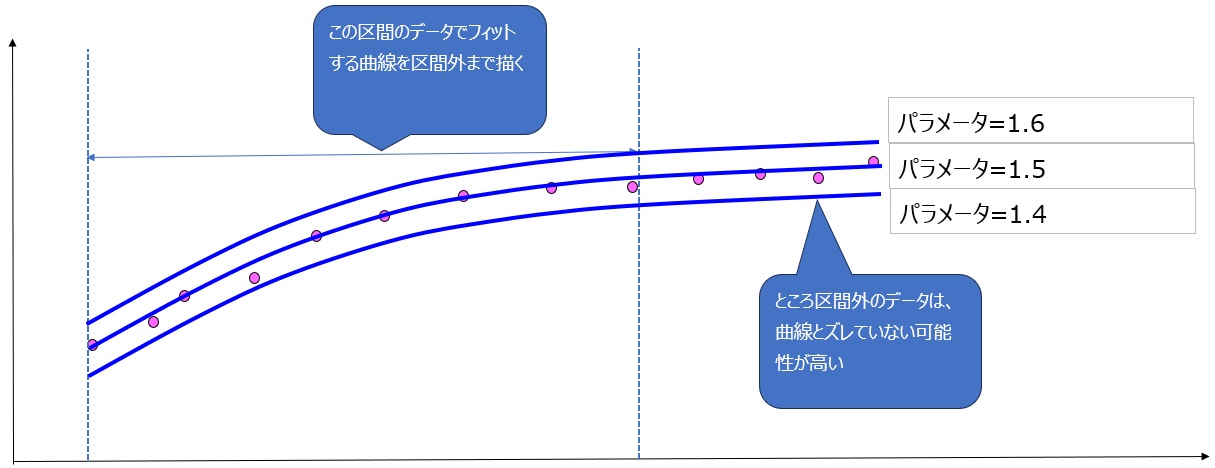
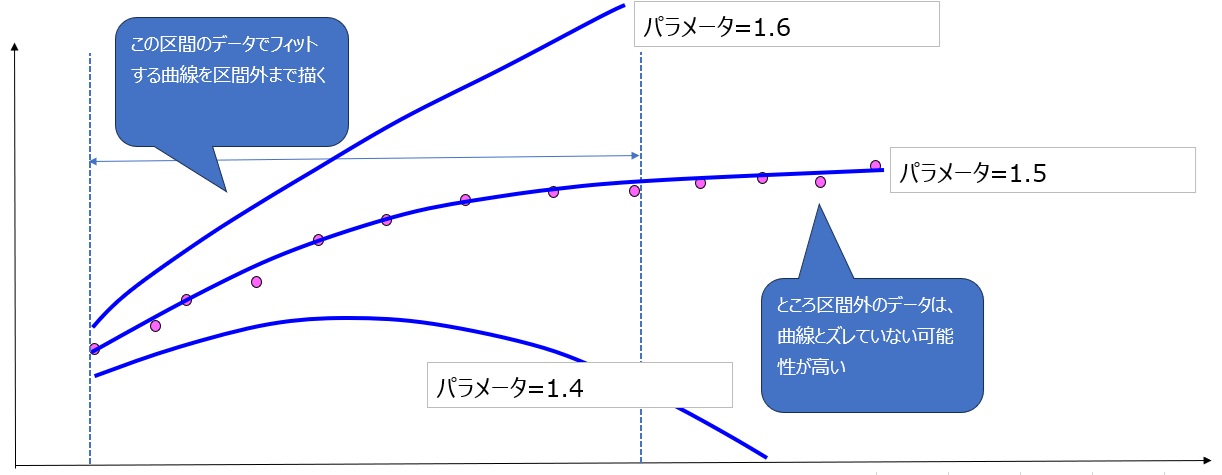
しかし、以下の図のようにパラメータの値を少し変えただけで結果が大きく変わる場合は、カーブフィッティングの可能性が高くなります。(※冒頭の注意参照)
このような分析は、パラメータ感度分析と言います。
②トレードルールの根拠が説明できること
作成したFXトレードルールについて、「なぜ効果があるのか」をしっかり説明できることは非常に重要です。
理由が明確であれば、過去データへの偶然の一致(カーブフィッティング)の可能性は低くなります。
ただし、説明できること=未来でも必ず利益が出るわけではありません。相場環境の変化には注意が必要です。
③別のデータで検証する(バックテスト+フォワードテスト)
まずは基本的な検証方法として、バックテストとフォワードテストがあります。
今まで説明してきた検証は、バックテストと言われるものです。
| 項目 | バックテスト | フォワードテスト |
|---|---|---|
| 使うデータ | 過去のチャート(すでに終わった値動き) | 基本的にはこれからのチャート(リアルタイム)。過去データを分割して前半をバックテスト、後半をフォワードテストとして使う方法もあります。 |
| 目的 | 「もしこのルールで過去にトレードしていたらどうなるか?」を確認 | 「実際にこれからの相場で使ったらどうなるか?」を試す |
| メリット | すぐに大量のデータで検証可能 | 現実の相場での動きを確かめられるため信頼性が高い |
| デメリット | 過去に合っただけで未来で通用するとは限らない | 時間がかかる(数週間〜数か月) |
| 例え話 | 模擬試験で過去問を解く | 本番試験を受ける |
バックテストは過去のチャートでルールの性能を確認し、フォワードテストは未知のデータで性能をチェックする方法です。
両方で安定した成績が出れば、「過去にたまたま合っただけ(カーブフィッティング)」である可能性は低くなります。
これは、バックテスト期間の相場環境が続く場合、同じように性能を発揮できるはずだからです。
もしフォワードテストで性能が発揮できない場合は、バックテスト期間にだけフィットしたルールであり、カーブフィッティングの可能性が高いと考えられます。
フォワードテストは本来、リアルタイムで行うのが基本ですが、時間がかかりすぎるという問題があります。
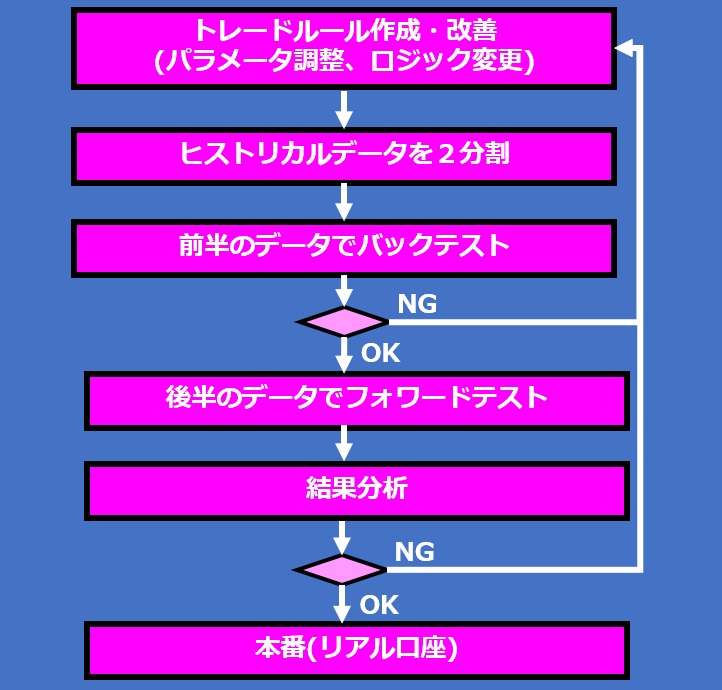
そのため、過去のヒストリカルデータを二分割して行う方法があります。
前半のデータを使ってパラメータ調整やロジック改善を繰り返し、トレードルールを確立します。
その後、後半のデータを使ってフォワードテストを行い、想定した性能が発揮できるかどうかを検証します。
データ量が少ない場合は、前8割をバックテストに、残り2割をフォワードテストに使用するケースもあります。
これで皆さん、確信を持てるでしょうか。
バックテスト+フォワードテストの弱点を挙げると、主に次の2点です。
| 弱点 | 内容 |
|---|---|
| 定性的な評価にとどまる | 見た目や成績の印象だけで判断しており、数値的・統計的に良し悪しを正確に評価することはできません。 |
| 過去データのノイズによる精度低下 | 実際のチャートには偶然の変動や特殊要因が含まれるため、バックテストやフォワードテストの結果にノイズが混ざり、正確な評価を妨げる可能性があります。 |
④統計的に強固な検証(モンテカルロ・シミュレーション)
私のおすすめは、モンテカルロ・シミュレーションです。
モンテカルロ・シミュレーションでは、例えば「未来の収益が95%の確率でこの範囲に収まる」といった分析が可能です。
この手法を用いることで、②で挙げたバックテスト+フォワードテストの弱点である、
- 定性的な評価にとどまる
- 過去データのノイズによる精度低下
を解消することができます。
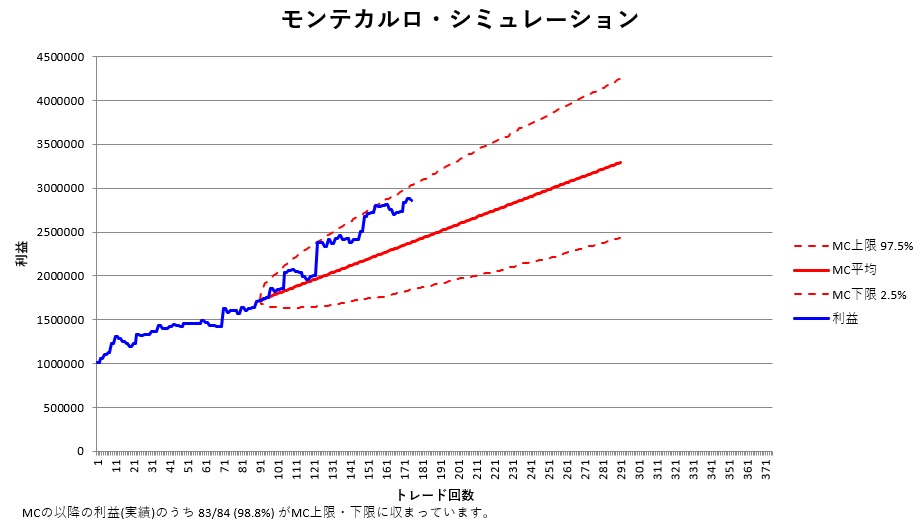
図の説明をすると、
- 青色の線(番号91まで):バックテスト結果
- 青色の線(番号91以降):フォワードテスト結果
- 赤色の点線:「未来の利益が95%の確率で収まる範囲」を示す
フォワードテスト期間の青線が赤点線内に収まっていれば、ルールの再現性・安定性が高いと判断できます。
さらに、フォワードテストの結果が赤線の内側にどのくらいの割合で含まれているかを計算すれば、カーブフィッティングでないことを定量的に評価できます。
今回の例では、フォワードテストの83/84=98.8%がモンテカルロ・シミュレーションの95%幅に含まれています。
95%以上であるため、このトレードルールはカーブフィッティングではないと判断できます。
また「過去データのノイズによる精度低下」についてですが、モンテカルロ・シミュレーションを使うことでノイズの影響を少なくすることが可能です。
95%の確率の幅で収益を予測しているため、極端なデータの影響を統計的に抑えることが可能であるためです。
モンテカルロ・シミュレーションに関する説明は長くなるため、この記事では割愛します。
別の記事で説明したいと思います。
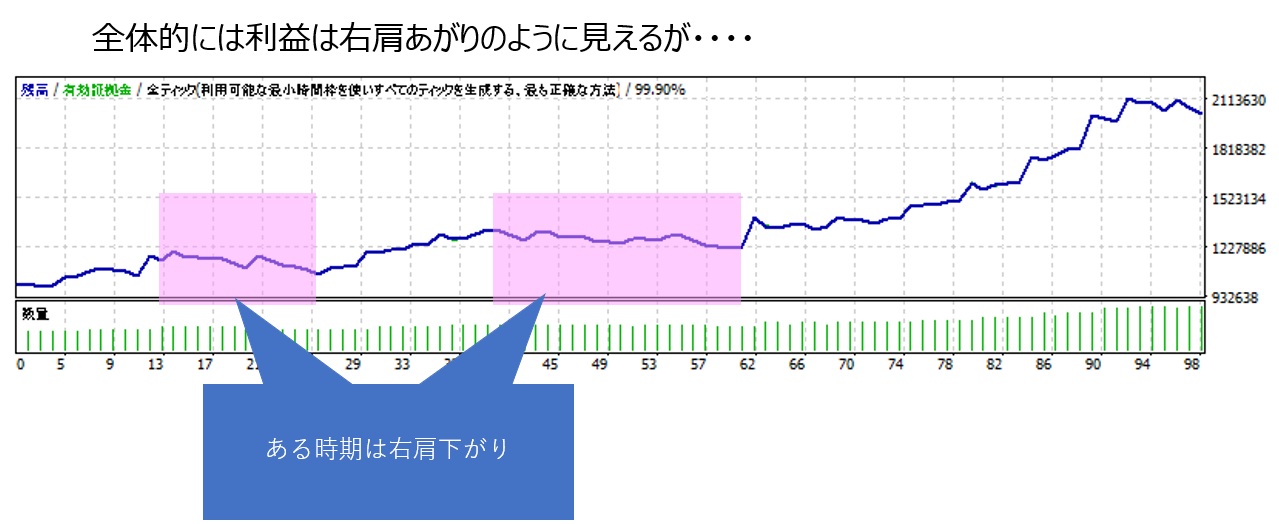
欠点としては、全体の利益は右肩上がりに見えても、細部で右肩下がりがある場合、この手法では評価されてしまうことがあります。
※ 詳しいやり方や計算方法は、別の記事で図解付きで解説します。今回は「何を確認するか」「なぜ重要か」を理解することが目的です。
さて、これで十分でしょうか。
の方法の欠点として、全体の利益曲線が右肩上がりに見えても、一部の期間では利益が右肩下がりになっている場合があります。
バックテスト+フォワードテスト+モンテカルロ・シミュレーションでは、こうした細部の下落が十分に評価されない可能性があります。
そのため、少なくとも年単位で利益がプラスであることを確認することが望ましいです。
⑤実運用に耐えられる安定性検証(モンテカルロ、二項検定、Wilsonスコア補正)
バックテストとフォワードテストにモンテカルロ・シミュレーションを組み合わせた評価で「過去のデータだけに合った偶然のルールではない」ことを定量的に評価できるようになりました。
これで安心してはいけません。
たとえば、全体の利益は上がっているように見えても、短い期間だけを見ると損失になっていることがあります。
こうした「小さな負けの期間」を無視すると、実際に運用したときに思わぬ損失を出す可能性があります。
そこで必要になるのが、「実際の運用でも安定して使えるか」を確かめる検証です。
検証方法:
. 利益の変動を分かりやすくする
まず、過去のデータを3か月ごとに区切って、利益が出たかどうかを1(利益あり)か0(損失あり)で記録します。
💡 なぜ3か月ごとなのか?
相場は常に変化しており、短期間だけの結果で判断すると「偶然勝っただけ」の可能性があります。
3か月程度の期間で区切ることで、短期の運の影響を減らし、ある程度まとまった相場の流れで利益が出るかどうかを確認できます。
つまり、「特定の一瞬だけ勝てたのではなく、複数の期間にわたって安定して利益が出るか」を見るためです。
2. 偶然で勝ったのかを統計でチェック
次に、統計的な方法を使って、「偶然で利益が出ただけではないか」を検証します。
私が実際に使った方法は、以下の3つです。
| 手法 | 概要 |
|---|---|
| モンテカルロ・シミュレーション | ランダム関数を使ったシミュレーションで確率を算出し、利益が出た割合が偶然ではないことを比較評価する方法 |
| 二項検定 | モンテカルロ・シミュレーションでは、ランダム関数で確率を算出したが二項定理では、数式を使って確率を算出し、利益が出た割合が偶然ではないことを比較評価する方法。基本的に結果は、モンテカルロ・シミュレーションとほぼ同じになるはずである。 |
| Wilsonスコア補正 | データが少ない場合でも、勝率の信頼性を判断できる補正 |
この3つともに偶然ではないという結果が出たときのみ、「偶然で勝っただけではない、本当に安定したトレードルール」を評価できます。
統計的に確認することで、偶然で勝っただけではない、安定したトレードルールかを評価できます。
※ 詳しいやり方や計算方法は、別の記事で図解付きで解説します。今回は「何を確認するか」「なぜ重要か」を理解することが目的です。
その他の検証方法
他には以下の方法があります。
| 手法 | 説明 | 目的・効果 |
|---|---|---|
| ウォークフォワード最適化 | 過去データを短期間ごとに分け、順番に最適化→検証を繰り返す方法 | ルールが長期にわたり安定して通用するかを確認する |
| 異なる通貨ペア・時間足での検証 | 作ったルールを別の通貨ペアや異なる時間足で試す | 特定の市場や時間帯だけに依存していないか確認する |
| シャッフルテスト | 過去データの順序をランダムに入れ替えてルールを適用する | 偶然のパターンで利益が出ていないかを確認する |
| ストレステスト | 急激な相場変動や極端な条件でルールを試す | 実際の運用で大きな損失が出ないか安全性を確認する |

